IEEE 浮点数表示
Contents
二进制小数
对于二进制小数的表示方法,按照十进制的表示方法,比较容易想到: 按每位的权值表示,小数部分依次表示$2^{-1}, 2^{-2}, 2^{-3} … $
即对于一个二进制数 $b_3 b_2b_1b_0.b_{-1}b_{-2}$ ,其十进制值为$$b_3 * 2^3 + b_2 * 2^2 + b_1 * 2^1 + b_0 * 2^0 . b_{-1} * 2^{-1} + b_{-2} * 2^{-2}$$ 比如123.45 可表示为 1111011.0111001100110011001100110011001100110011001101,当然这样并不能表示所有小数,只能近似,上述二进制实际转换回来是 123.45000000000027285。
IEEE 754
为了表示更大的数,十进制可以采用科学计数法$ a * 10^b$的形式,同样的 IEEE浮点数标准用下面的方式来表示浮点数
$$V = (-1)^s * M * 2^E$$
在实际的32bit float的存储格式为下图:

32-bit floating point
肉眼可见的分三部分,对应IEEE浮点数中的s 、E 、M。
- 第一部分:sign 1bit 符号位,0表示正数,1表示负数。
- 第二部分:exponent 8bits (简称e) 表示 E, 具体怎么表示的见后面
- 第三部分: fraction 23bits (简称f) 表示 M, 具体怎么表示的见后面
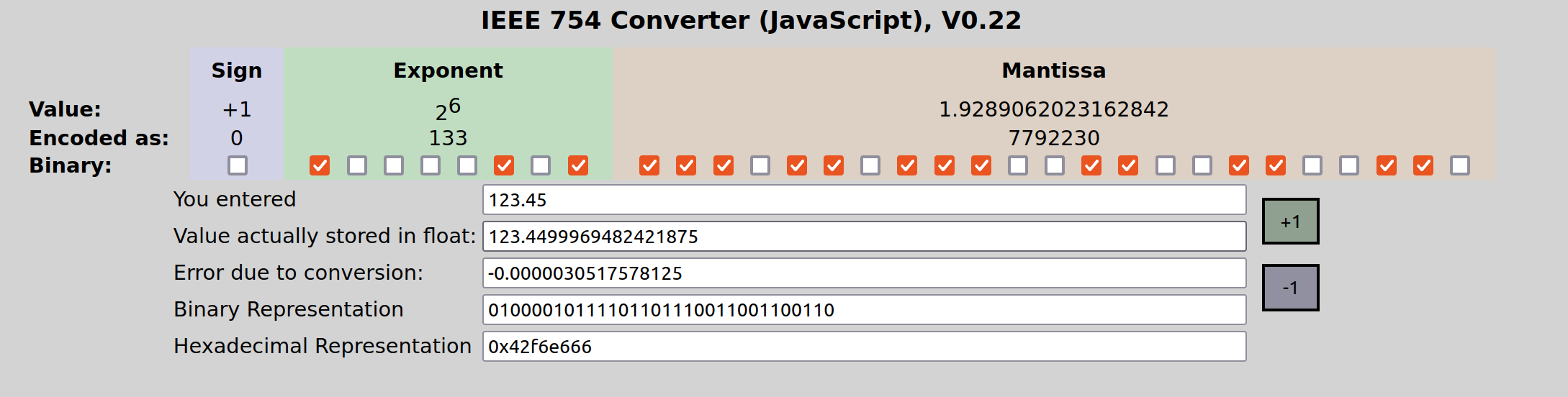
一个浮点数如何用IEEE浮点数表示? 还以123.45为例子:
其二进制表示为
$$1111011.0111001100110011001100110011001100110011001101$$
按照科学计数法的表示习惯为可以表示为: $$1.1110110111001100110011001100110011001100110011001101 * 2^6 $$ 看这个就是前面的式子$M * 2^E$。
但实际存储的时候,IEEE浮点数标准还规定:
- 在这种情况下, M 的总是1.几,实际存储时候整数1可以省略,所以M定义为1+f (即此处, f = 1110110111001100110011001100110011001100110011001101)。
- 在这种情况下, e = E + Bias, 其中$Bias = 2^{k-1} - 1$, $k$为exponent的位数,对于float而言, $Bias = 2^{8 - 1} - 1 = 127$。(此处E=6,可得 $e = 6 + 127 = 133 = (10000101)_2$)
所以对于123.45的IEEE浮点数按照格式填入,fraction省略23bit之后的,可得:
0 10000101 11101101110011001100110
s e f
找一个IEEE 754在线转换网站,输入123.45,得到的值和计算的一致。
123.45
在IEEE浮点数标准中,以上属于“规格化数”情况,如果按这种方式计算M最小取1,E最小取-127,则我们最小能表示的最接近0的浮点数为$\pm2^{-127}$。
所以IEEE规定当一个数字的绝对值小于$2^{-126}$时 使用“非规格化数”表示:
- exponent(e)全为0,定义$E = 1 - Bias$,且M=f,即只有小数。 这样就可以表示0,以及那些非常接近与0.0的数。(此处float的 E = 1 - 127 = -126, 即非规格化数$<\pm2^{-126}$和规格化数最小为$\pm2^{1 - 127} = \pm2^{-126}$刚好衔接)
以$2^{-128}$为例, $2^{-128} = M * 2^E = 2^{-2} * 2^{-126} $ ,即$ M = 2^{-2}$ ,实际存储的值为:
0 00000000 01000000000000000000000
s e f
除此之外的情况就是无穷大和NaN:
- exponent(e)全为1, fraction(f)全为0时,表示无穷,f为非零时表示NaN(不是一个数)。
参考
https://zh.m.wikipedia.org/zh/IEEE_754
https://www.bilibili.com/video/BV1cr4y1n7Ps